266. Graph Implementation – Adjacency Matrix | Set 3

Earlier we had discussed in Graph Representation – Adjacency Matrix and Adjacency List about Graph and its different representations and we read Graph Implementation – Adjacency List .In this article we will implement graph using adjacency matrix.

We would recommend to read the theory part of Graph Representation – Adjacency Matrix and Adjacency List before continue reading this article.

Let’s revise few basic concepts:

What is Graph:

G = (V,E)

Graph is a collection of nodes or vertices (V) and edges(E) between them. We can traverse these nodes using the edges. These edges might be weighted or non-weighted.

Adjacency Matrix:

Adjacency Matrix is 2-Dimensional Array which has the size VxV, where V are the number of vertices in the graph. See the example below, the Adjacency matrix for the graph shown above.

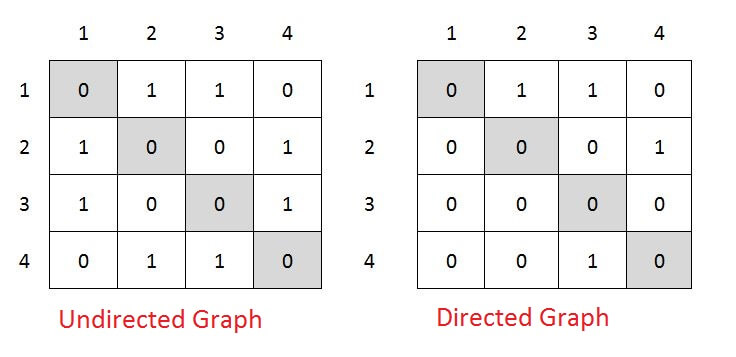
1. adjMaxtrix[i][j] = 1 when there is edge between Vertex i and Vertex j, else 0.
2. It’s easy to implement because removing and adding an edge takes only O(1) time.
3. But the drawback is that it takes O(V²) space even though there are very less edges in the graph.

Output:

Graph: (Adjacency Matrix)
0 1 0 0 1
1 0 1 1 1
0 1 0 1 0
0 1 1 0 1
1 1 0 1 0
Vertex 0 is connected to:1 4
Vertex 1 is connected to:0 2 3 4
Vertex 2 is connected to:1 3
Vertex 3 is connected to:1 2 4
Vertex 4 is connected to:0 1 3

Related Problems:

- Graph – Software Installation Problem Medium
- Graph – Detect Cycle in a Directed Graph Medium
- Topological Sort Medium
- Dijkstra’s – Shortest Path Algorithm (SPT) – Adjacency List and Priority Queue – Java Implementation Hard