|
Be the first user to complete this post
|
Add to List |
405. Evaluation of Postfix Expressions (Polish Postfix notation) | Set 1
Postfix notation is a notation for writing arithmetic expressions in which the operands appear before their operators. There are no precedence rules to learn, and parentheses are never needed. Because of this simplicity.
Let's assume the below
- Operands are real numbers in single digits. (Read: Evaluation of Postfix Expressions for any Number )
- Permitted operators: +,-, *, /, ^(exponentiation)
- Blanks are NOT permitted in expression.
- Parenthesis are permitted
Example:
Postfix: 54+ Output: 9 Explanation: Infix expression of above postfix is: 5+ 4 which resolves to 9 Postfix: 2536+**5/2- Output: 16 Explanation: Infix expression of above postfix is: 2 * (5 *(3+6))/5-2 which resolves to 16
Approach: Use Stack
Algorithm:
Iterate through given expression, one character at a time
- If the character is an operand, push it to the operand stack.
- If the character is an operator,
- pop an operand from the stack, say it's s1.
- pop an operand from the stack, say it's s2.
- perform (s2 operator s1) and push it to stack.
- Once the expression iteration is completed, The stack will have the final result. Pop from the stack and return the result.
Please see the walkthrough of an example below for more understanding.
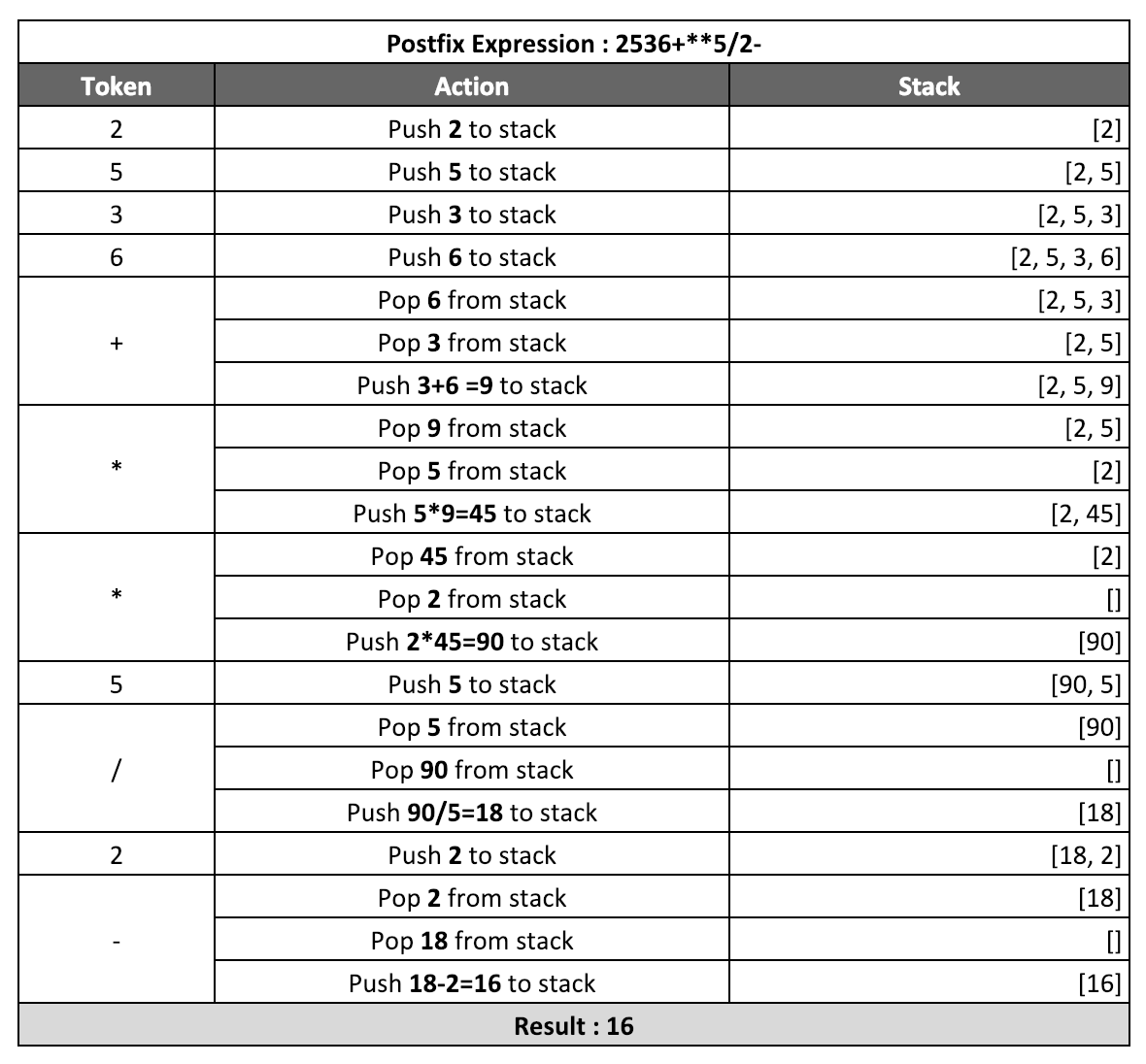
Output:
Postfix Expression: 2536+**5/2- Evaluation: 16.0
PS: In this article, we have discussed an approach to evaluate postfix expressions where operands are of single digits. In the next article, we will extend to multiple digits using some separator. Click here to read about - Evaluation of Postfix Expressions for any Number

