Be the first user to complete this post

  • 0
 Add to List
Hard

129. Binary Min-Max Heap Implementation

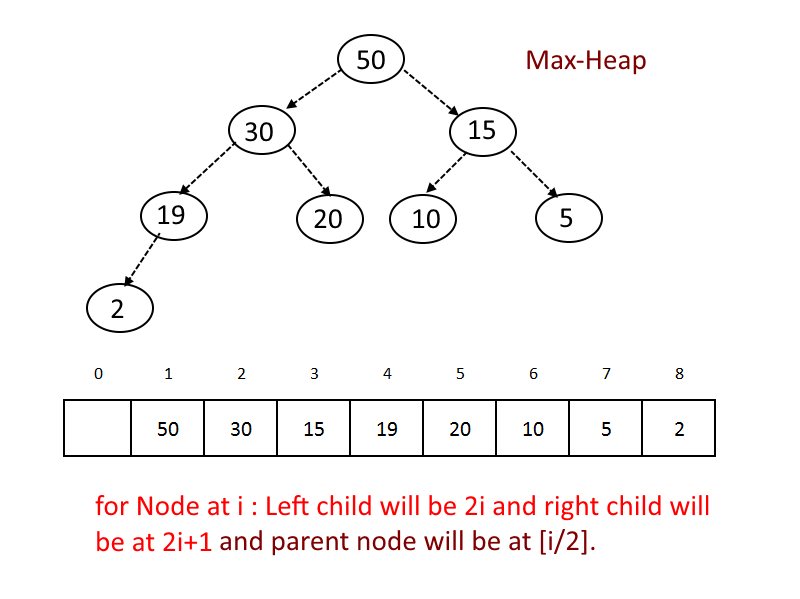
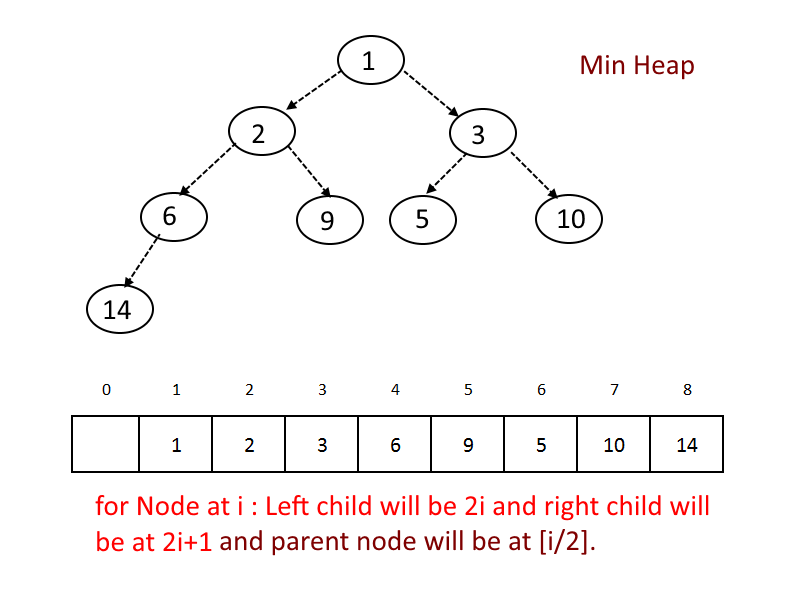
A binary heap is a heap data structure created using a binary tree.

binary tree has two rules -

  1. Binary Heap has to be a complete binary tree at all levels except the last level. This is called a shape property.
  2. All nodes are either greater than equal to (Max-Heap) or less than equal to (Min-Heap) to each of its child nodes. This is called heap property.

Implementation:

  1. Use an array to store the data.
  2. Start storing from index 1, not 0.
  3. For any given node at position i:
  4. Its Left Child is at [2*i] if available.
  5. Its Right Child is at [2*i+1] if available.
  6. Its Parent Node is at [i/2]if available.
Max-Heap
Max-Heap
Min-Heap
Min-Heap

Heap Majorly has 3 operations -

  1. Insert Operation
  2. Delete Operation
  3. Extract-Min (OR Extract-Max)

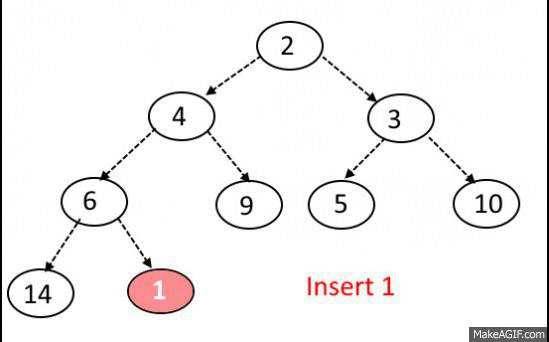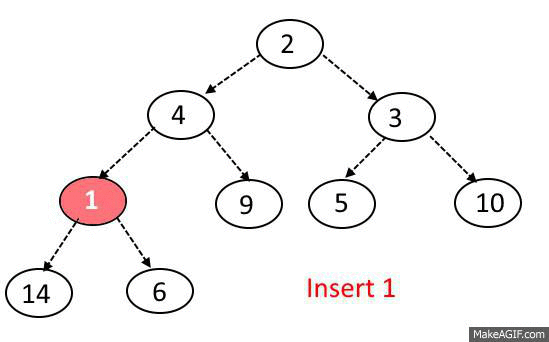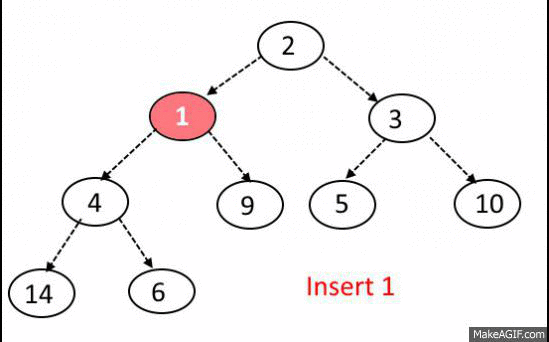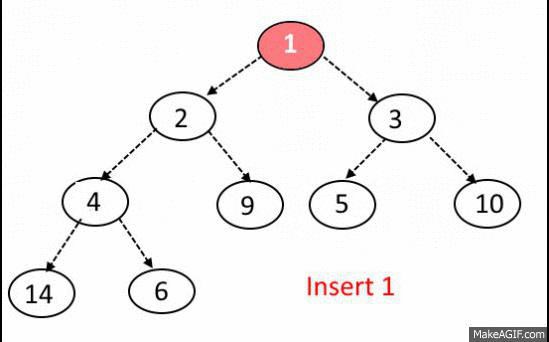
Insert Operation:

  1. Add the element at the bottom leaf of the Heap.
  2. Perform the Bubble-Up operation.
  3. All Insert Operations must perform the bubble-up operation(it is also called as up-heap, percolate-up, sift-up, trickle-up, heapify-up, or cascade-up)
Insert() - Bubble-Up Min-Heap
Insert() - Bubble-Up Min-Heap

Extract-Min OR Extract-Max Operation:

  1. Take out the element from the root.( it will be minimum in case of Min-Heap and maximum in case of Max-Heap).
  2. Take out the last element from the last level from the heap and replace the root with the element.
  3. Perform Sink-Down
  4. All delete operations must perform Sink-Down Operation ( also known as bubble-down, percolate-down, sift-down, trickle-down, heapify-down, cascade-down).

Sink-Down Operation:

  1. If the replaced element is greater than any of its child node in case of Min-Heap OR smaller than any if its child node in case of Max-Heap, swap the element with its smallest child(Min-Heap) or with its greatest child(Max-Heap).
  2. Keep repeating the above step, if the node reaches its correct position, STOP.
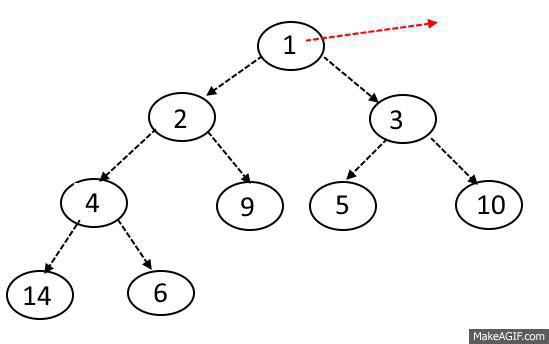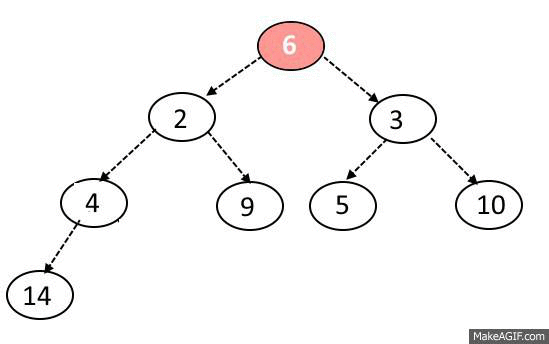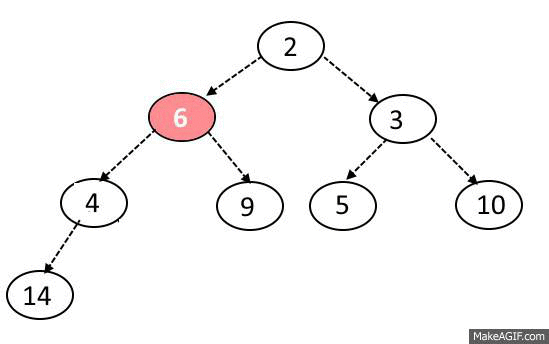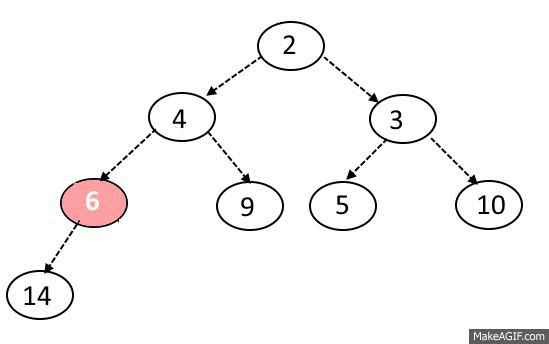
Delete OR Extract Min from Heap
Delete OR Extract Min from Heap

Delete Operation:

  1. Find the index for the element to be deleted.
  2. Take out the last element from the last level from the heap and replace the index with this element .
  3. Perform Sink-Down

Time and Space Complexity:

SpaceO(n)
SearchO(n)
InsertO(log n)
DeleteO(log n)

Output:

Original Array : 3 2 1 7 8 4 10 16 12
Min-Heap : 1 3 2 7 8 4 10 16 12
Sorted: 1 3 2 12 8 4 10 16 0

Related Problems: